Concetti fondamentali
In questa sezione verranno analizzati alcuni concetti fondamentali riguardo i sistemi crittografici che vedremo più avanti, i concetti sono:
- Security through obscurity
- Bits of security
- Confusion and Diffusion
- Perfect Cipher
Security through obscurity
Portiamo alcuni esempi di sistemi crittografici insicuri per introdurre alcuni concetti chiave della crittografia. Immaginiamo il seguente algoritmo di cifratura: per cifrare un messaggio, si sostituisce ogni lettera con la lettera 3 posizioni più avanti nell'alfabeto. Ad esempio, la lettera 'A' diventa 'D', 'B' diventa 'E', la 'Z' diventa 'C' ecc.
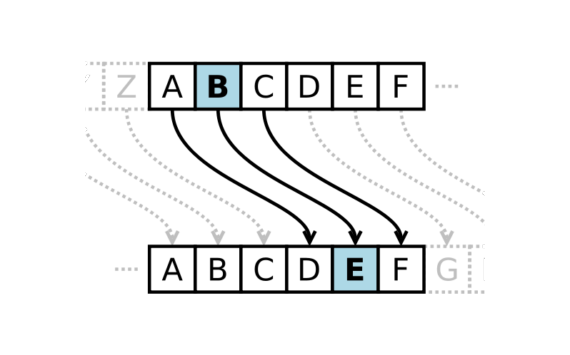
Questo cifrario è noto come cifrario di Cesare, perché fu utilizzato da Giulio Cesare per comunicazioni segrete.
Immaginiamo di voler cifrare il seguente messaggio: attaccare all'alba; togliendo la punteggiatura e gli spazi il messaggio cifrato diventa: dwwdffduhdoodoed. Una volta ricevuto il messaggio cifrato, il destinatario può decifrarlo semplicemente spostando ogni lettera di tre posizioni all'indietro nell'alfabeto. Durante il transito il messaggio è apparentemente incomprensibile, dunque sembrebbe essere un buon metodo di cifratura. Tuttavia la segretezza del messaggio è basata sulla segretezza dell'algoritmo, un attaccante che conosce il metodo di cifratura può facilmente decifrare il messaggio.
Questa pratica è nota appunto come sicurezza tramite segretezza (security through obscurity) e non è considerata un metodo sicuro di cifratura. La crittografia moderna si basa su algoritmi crittografici ben definiti e pubblici, la sicurezza dei dati non dipende dalla segretezza dell'algoritmo ma dalla segretezza della chiave.
Un gran numero di sistemi crittografici per le telecomunicazioni e la gestione dei diritti digitali che utilizzavano la sicurezza tramite segretezza alla fine sono stati compromessi.
Bits of security
Dunque un algoritmo di cifratura deve avere come parametro una chiave, segreta tra le parti comunicanti, che permette di cifrare e decifrare i messaggi. Dovesse essere scoperta la chiave le parti comunicanti possono cambiare la chiave e continuare a comunicare in sicurezza. Con questa premessa possiamo modificare il cifrario di Cesare in modo da utilizzare una chiave: la chiave sarà un numero intero compreso tra 0 e 25 (alfabeto inglese) che indica di quante posizioni spostare le lettere nell'alfabeto; chiamiamo questo algoritmo ROTK. Con chiave "3" si ottiene esattamente il cifrario di Cesare.

Anche in questo caso l'algoritmo di cifratura è insicuro e facilmente attaccabile, un attaccante può semplicemente provare tutte le chiavi possibili fino a trovare una chiave che decifri il messaggio in un testo comprensibile. Questo attacco è noto come attacco a forza bruta e la sua fattibilità dipende dal numero di chiavi possibili, nel caso di ROTK sono solamente 26, decisamente poche per garantire sicurezza contro attacchi a forza bruta. Un algoritmo crittografico sicuro deve avere un numero di chiavi possibili tale da rendere impraticabile un attacco a forza bruta, il modo più comune per misurare la sicurezza di un algoritmo crittografico è il numero di bit di sicurezza (bits of security). Un algoritmo ha \(n\) bit di sicurezza se occorrono \(2^n\) operazioni per romperlo. Per dare una idea di ordine di grandezza, un algoritmo con 128 bit di sicurezza è considerato altamente sicuro.
Confusion and Diffusion
Dunque per quanto detto precedentemente occorre un algoritmo di cifratura che abbia una chiave come parametro, e questa chiave deve poter assumere un numero sufficientemente grande di valori per garantire sicurezza contro attacchi a forza bruta.
Introduciamo il seguente cifrario: utilizziamo come chiave una permutazione casuale dell'alfabeto, per ogni lettera del messaggio in chiaro sostituiamo con la lettera nella stessa posizione nella permutazione. Ad esempio supponendo che la chiave sia la permutazione UZSIAFXGQLKRMPHNBTOJEVWYDC la lettera 'A' sarà cifrata con 'U', 'B' con 'Z', 'C' con 'S' ecc. Il messaggio attaccare all'alba cifrato con questa chiave diventa UJJUSSUTAURRURZU. Questo cifrario è noto come cifrario a sostituzione monoalfabetica, vediamo se ha un sufficiente numero di bit di sicurezza. L'alfabeto inglese ha 26 lettere, dunque il numero di chiavi possibili è \(26!\) (26 fattoriale) che è circa \(2^{88}\), dunque il cifrario di sostituzione monoalfabetica ha circa 88 bit di sicurezza, un numero sufficientemente grande per garantire sicurezza contro attacchi a forza bruta.
In questo caso l'algoritmo si può considerare sicuro? Anche in questo caso un attaccante può decifrare il messaggio senza conoscere la chiave, l'idea di base è la seguente: un testo in italiano (ma vale per ogni lingua) ha una distribuzione delle lettere non uniforme, alcune lettere sono più frequenti di altre, e su testi ragionevolmente lunghi (è sufficiente qualche paragrafo) questa distribuzione risulta sempre uguale. Dunque sapendo che nella lingua italiana la lettera che compare più frequentemente è la e, si può assumere che nel testo cifrato la lettera più frequente corrisponda alla e, e cosi' via per le altre lettere. Questo attacco è noto come attacco per analisi delle frequenze e permette di decifrare il messaggio senza conoscere la chiave.
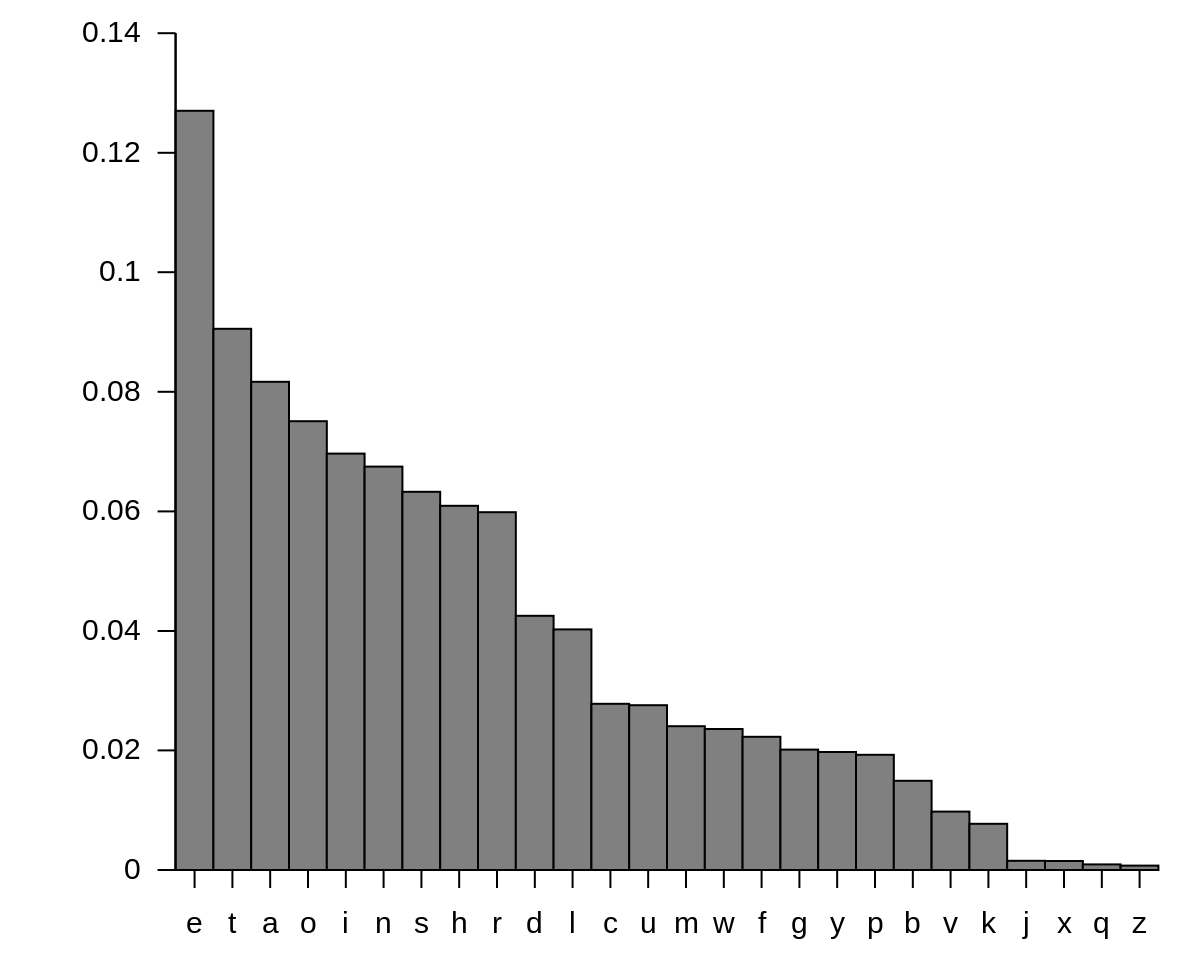
A primo impatto questo metodo può sembrare poco convincente, ma effettivamente funziona come descritto sopra; esistono numerosi tool online che permettono di decifrare testi cifrati con sostituzione monoalfabetica, ad esempio dcode.fr. Dato il seguente testo cifrato:
QPBEAOJHSUOHRURXHTQJMHOQNEHSHPOQIATUTAOQSETHUPSGAQPBEAOJHSUOHEPUJJUSSUPJANEHIASQFTUTAQRMAOOUXXQHOAPCUSHPHOSATARUSGQUVARQIAUIQZUOAARUOAXEAPJAEPJAOJHQPQJURQUPHMUVURANATHXPQRQPXEUGUEPUIQOJTQZECQHPAIARRARAJJATAPHPEPQFHTMAURSEPARAJJATAOHPHNQEFTABEAPJQIQURJTAAOEJAOJQTUXQHPAVHRMAPJAREPXGQAOEFFQSQAPJABEURSGANUTUXTUFHBEAOJUIQOJTQZECQHPATQOERJUOAMNTAEXEURAIEPBEAOUNAPIHSGAPARRURQPXEUQJURQUPURURAJJATUSGASHMNUTANQEFTABEAPJAMAPJAARUAOQNEHUOOEMATASGAPARJAOJHSQFTUJHRURAJJATUNQEFTABEAPJASHTTQONHPIUURRUAASHOQVQUNATRAURJTARAJJATABEAOJHUJJUSSHAPHJHSHMAUJJUSSHNATUPURQOQIARRAFTABEAPCAANATMAJJAIQIASQFTUTAQRMAOOUXXQHOAPCUSHPHOSATARUSGQUVA
è possibile decifrarlo in un istante attraverso il tool appena citato. La debolezza di questo cifrario risiede nel fatto che mantiene le proprieta' statistiche del messaggio originario, un cifrario sicuro deve produrre un testo cifrato che sia indistinguibile da un testo casuale. Questo concetto è noto come confusione e diffusione (confusion and diffusion) e rappresenta un principio fondamentale della crittografia moderna. Nelle definizioni originali di Shannon, la confusione si riferisce a rendere la relazione tra il testo cifrato e la chiave simmetrica il più complessa e intricata possibile; la diffusione si riferisce a dissipare la struttura statistica del testo in chiaro su tutto il testo cifrato.
Tutti gli algoritmi crittografici moderni sono progettati per garantire le proprietà discusse in questo capitolo, per portare un esempio che verrà approfondito in seguito, l'algoritmo AES (Advanced Encryption Standard) è uno dei più utilizzati algoritmi di cifratura simmetrica; l'algoritmo è di pubblico dominio ed ha una chiave di 128 bit (o più) dunque è sicuro contro attacchi a forza bruta, inoltre è progettato per garantire confusione e diffusione.
Perfect Cipher
In crittografia, un perfect cipher è un sistema di cifratura che è teoricamente sicuro, cioè un attaccante non può decifrare il messaggio cifrato senza conoscere la chiave, indipendentemente dalla potenza computazionale. Il più noto esempio di perfect cipher è il One-Time Pad (OTP). Un OTP utilizza una chiave casuale, lunga quanto il messaggio da cifrare, e ciascuna chiave viene utilizzata solo una volta. Il messaggio viene cifrato combinando ciascun bit del messaggio con il bit corrispondente della chiave tramite l'operazione di XOR.
Lo XOR (o esclusivo OR) è un'operazione logica che funziona su coppie di bit. La seguente è la tabella di verità dello xor (spesso riassunta con: 1 se i due bit sono diversi e 0 se i due bit sono uguali):
| \(A\) | \(B\) | \(A \oplus B\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
E seguono direttamente le seguenti proprietà:
- Commutatività: \( A \oplus B = B \oplus A \)
- Associatività: \( (A \oplus B) \oplus C = A \oplus (B \oplus C) \)
- Identità: \( A \oplus 0 = A \)
- Involutività: \( A \oplus A = 0 \)
Per cifrare un messaggio con un OTP, si esegue l'operazione XOR tra ciascun bit del messaggio e il bit corrispondente della chiave. Per decifrare il messaggio, si esegue di nuovo l'operazione XOR tra il messaggio cifrato e la stessa chiave. Il sistema crittografico funziona perché si ha \(C = M \oplus K\), \(M = C \oplus K = (M \oplus K) \oplus K = M \oplus (K \oplus K) = M\) (con C si intende il crittogramma, con M il messaggio e con K la chiave).
Ad esempio, se il messaggio è 1101 e la chiave è 1011, il messaggio cifrato sarà 1100. Decifrando 1100 con la chiave 1011 si ottiene di nuovo 1101. Questo metodo garantisce che il messaggio cifrato non riveli alcuna informazione sul messaggio originale senza conoscere la chiave, rendendo l'OTP un perfect cipher se la chiave è davvero casuale, della stessa lunghezza del messaggio e utilizzata una sola volta. Per convincerci di ciò immaginiamo di effettuare un attacco forza bruta contro il testo cifrato, ossia proviamo a decifrare con tutti i valori possibili della chiave:
| crittogramma | chiave | messaggio |
|---|---|---|
| 0110 | 0000 | 0110 |
| 0110 | 0001 | 0111 |
| 0110 | 0010 | 0100 |
| 0110 | 0011 | 0101 |
| 0110 | 0100 | 0010 |
| 0110 | 0101 | 0011 |
| 0110 | 0110 | 0000 |
| 0110 | 0111 | 0001 |
| 0110 | 1000 | 1110 |
| 0110 | 1001 | 1111 |
| 0110 | 1010 | 1100 |
| 0110 | 1011 | 1101 |
| 0110 | 1100 | 1010 |
| 0110 | 1101 | 1011 |
| 0110 | 1110 | 1000 |
| 0110 | 1111 | 1001 |
Osserviamo che nella colonna del messaggio otteniamo tutti i messaggi possibili di lunghezza 4, ovviamente tra questi è presente anche il messaggio originale ma a priori non è possibile in alcun modo distinguerlo dagli altri. L'esempio con messaggi di 4 bit è chiaramente poco realistico ma serve per dare l'intuizione che, anche con messaggi di lunghezza arbitraria, non vi è alcun modo per estrarre informazioni sul messaggio in chiaro se è stato cifrato con OTP.
Il problema di OTP è che necessita di una chiave lunga quanto il messaggio, è chiaro che questo in molti casi può risultare problematico, ed è il motivo per cui in pratica OTP non viene utilizzato.
Da notare che il problema della lunghezza della chiave è proprio la proprietà che lo rende un cifrario perfetto, tentare di usare una chiave più corta, per esempio ripetendola ciclicamente rende il cifrario insicuro. Vediamo in un esempio come mai questo accade: se il messaggio è \(m_0, m_1, m_2, m_3\) ma la chiave è \(k_0, k_1\) e per coprire tutto il messaggio viene ripetuta un volta, in modo da ottenere \(k_0, k_1, k_0, k_1\), cifrando i bit del crittogramma saranno: \(m_0 \oplus k_0, m_1 \oplus k_1, m_2 \oplus k_0, m_3 \oplus k_1\). Adesso effettuando lo XOR tra il primo e il terzo bit ed il secondo con il quarto bit del crittogramma otteniamo:
- \(c_0 \oplus c_2\) = \((m_0 \oplus k_0) \oplus (m_2 \oplus k_0)\) = \(m_0 \oplus m_2\)
- \(c_1 \oplus c_3\) = \((m_1 \oplus k_1) \oplus (m_3 \oplus k_1)\) = \(m_1 \oplus m_3\)
dunque otteniamo delle informazioni sul testo in chiaro, che in alcuni casi possono essere sufficienti a decifrare tutto o parte del messaggio.