Firme digitali
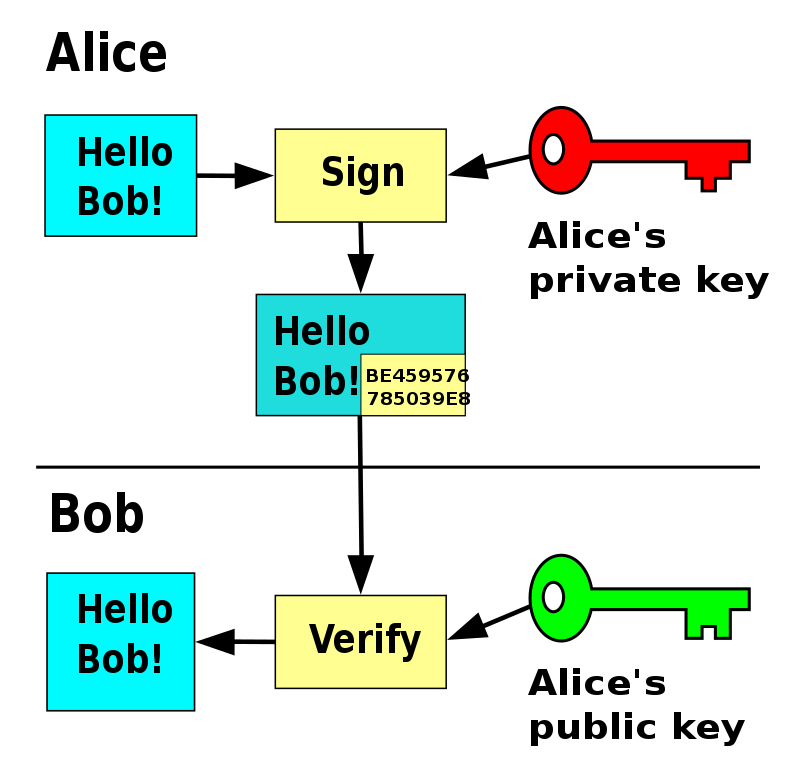
Una firma digitale è uno schema matematico per verificare l'autenticità di messaggi o documenti digitali. Una firma digitale valida su un messaggio offre al destinatario la certezza che il messaggio provenga da un mittente noto al destinatario. Nello specifico, le firme digitali garantiscono le seguenti proprietà:
-
Autenticità: garantisce che un messaggio o documento provenga realmente dall'emittente dichiarato. Le firme digitali assicurano questa proprietà, poiché solo il possessore della chiave privata può generare una firma verificabile con la chiave pubblica corrispondente.
-
Integrità: assicura che il contenuto di un messaggio o documento non sia stato modificato durante la trasmissione. Le firme digitali e le funzioni hash crittografiche permettono di rilevare qualsiasi alterazione nei dati.
-
Non Ripudiabilità: impedisce all'emittente di negare di aver inviato un messaggio o effettuato una transazione. Le firme digitali forniscono questa proprietà, poiché la firma è generata con la chiave privata dell'emittente, rendendo impossibile la negazione da parte sua.
In modo simile a quanto visto per RSA, vi sono una coppia di chiavi legate da una relazione matematica tali che una chiave è utilizzata per firmare i messaggi (chiave privata) e l'altra per verificarli (chiave pubblica).
Firme con RSA
Portiamo un esempio di sistema di firma digitale basato su RSA. La generazione della coppia di chiavi funziona come visto precedentemente con e nel complesso il processo funziona in questo modo:
- Alice genera due numeri primi grandi \(p\) e \(q\) e calcola \(n = p \cdot q\).
- Alice sceglie un numero \(e\) e rende pubblica la coppia \((n, e)\), questa è la chiave pubblica.
- Alice calcola \(d\) tale che \(e \cdot d = 1 \mod \phi(n)\), dove \(\phi(n) = (p-1) \cdot (q-1)\), \(d\) è la chiave privata.
- Alice firma un messaggio \(m\) con la chiave privata calcolando \(s = m^d \mod n\).
- Bob riceve il messaggio e la firma e verifica la firma calcolando \(m = s^e \mod n\).
La correttezza del processo di verifica della firma è garantita dalla stessa relazione matematica che garantisce la correttezza della decifratura dei messaggi cifrati con RSA. Infatti dato il messaggio \(m\) e la chiave pubblica \((n, e)\) è non c'è modo di trovare velocemente la quantità \(s\) tale che \(m = s^e \mod n\) senza conoscere la chiave privata \(d\). Notare che trovare \(s\) noto \(m\) equivale a trovare il messaggio conoscendo il crittogramma in RSA, quindi la sicurezza del sistema è basata sull'assunzione che non esista un algoritmo efficiente per fattorizzare numeri grandi.
In realtà non si firma mai direttamente il messaggio, ma si firma l'hash del messaggio. Questo perché le firme digitali sono spesso utilizzate per firmare documenti di grandi dimensioni e calcolare la firma su un hash è molto più efficiente. Le funzioni hash saranno discusse nei capitoli successivi.
Questo algoritmo rende chiara l'idea di come funzionano le firme digitali, tuttavia nel mondo reale si utilizzano protocolli più sofisticati come DSA (o la sua variante su curve ellittiche ECDSA).