Cifrari a chiave pubblica
Nei cifrari a chiave pubblica ogni utente possiede una coppia di chiavi: una chiave pubblica e una chiave privata. La chiave pubblica è accessibile a tutti, mentre la chiave privata è nota solo al proprietario. La chiave pubblica viene utilizzata per cifrare i messaggi, mentre la chiave privata viene utilizzata per decifrarli. Questo permette a chiunque di inviare messaggi cifrati all'utente, che può decifrarli solo con la propria chiave privata.
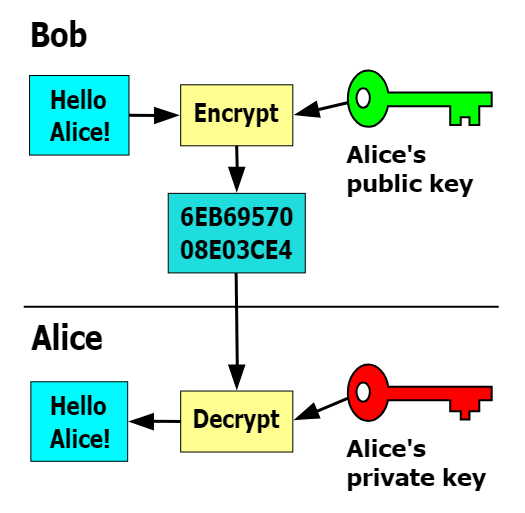
Il cifrario a chiave pubblica più noto è il cifrario RSA, che prende il nome dai suoi inventori Rivest, Shamir e Adleman.
RSA
Anche RSA come Diffie-Hellman funziona utilizzando la matematica modulare, tramite alcune proprietà dell'algebra modulare è possibile costruire una trapdoor function. Nella crittografia, una trapdoor function è una funzione che è facile da calcolare in una direzione, ma difficile da calcolare nella direzione opposta (trovare il suo inverso) senza informazioni speciali, chiamate trapdoor. Vediamo una rapida panoramica di come funziona RSA, anche in questo caso alcuni dettagli tecnici saranno omessi a favore una spiegazione intuitiva. I passaggi dell'algoritmo sono i seguenti:
- Alice genera due numeri primi grandi \(p\) e \(q\) e calcola \(n = p \cdot q\).
- Alice sceglie un numero \(e\) e rende pubblica la coppia \((n, e)\), questa è la chiave pubblica.
- Alice calcola \(d\) tale che \(e \cdot d = 1 \mod \phi(n)\), dove \(\phi(n) = (p-1) \cdot (q-1)\), \(d\) è la chiave privata.
- Bob cifra un messaggio \(m\) con la chiave pubblica di Alice calcolando \(c = m^e \mod n\).
- Alice decifra il messaggio calcolando \(m = c^d \mod n\).
Il passaggio numero 3 potrebbe sembrare un po' oscuro, il motivo per cui \(d\) viene calcolato in quel modo è che \(m^{ed} = m \mod n\) se e solo se \(e \cdot d = 1 \mod \phi(n)\), questo è un risultato noto come generalizzazione del piccolo teorema di Fermat. La cosa importante è che la quantità \(d\) si può calcolare facilmente solamente conoscendo la fattorizzazione di \(n\), e come detto precedentemente non esiste un algoritmo efficiente per fattorizzare numeri grandi.
Facciamo un esempio con numeri piccoli per capire meglio il funzionamento di RSA:
- Alice sceglie due numeri primi \(p = 61\) e \(q = 53\), calcola \(n = 61 \cdot 53 = 3233\).
- Alice sceglie \(e = 17\) e rende pubblica la coppia \((n, e) = (3233, 17)\).
- Alice calcola \(d = 2753\) (calcolato con l'algoritmo di Euclide esteso) e mantiene segreta la coppia \((n, d)\).
- Bob vuole inviare il messaggio \(m = 1234\) ad Alice, calcola \(c = 1234^{17} \mod 3233 = 2183\).
- Alice riceve il messaggio cifrato \(c = 2183\) e lo decifra calcolando \(m = 2183^{2753} \mod 3233 = 1234\).
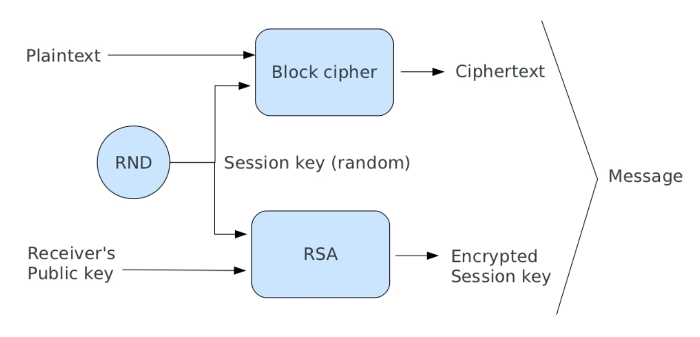
Una osservazione da fare è che con RSA è possibile cifrare solamente messaggi di lunghezza inferiore alla lunghezza della chiave. Per cifrare messaggi più lunghi si potrebbe pensare di dividere il messaggio in blocchi più piccoli e cifrarli singolarmente, tuttavia RSA non è progettato per cifrare grandi quantità di dati, in quanto è molto più lento rispetto ai cifrari simmetrici. In pratica si utilizza RSA per cifrare una chiave casuale e si utilizza il cifrario simmetrico per cifrare i dati. Questa tecnica è conosciuta come envelope encryption ed è utilizzata da numerosi protocolli crittografici moderni, alcuni esempi verranno discussi nei capitoli successivi.