Scambio di Chiavi
Il problema dello scambio di chiavi è uno dei problemi fondamentali della crittografia. Se due parti vogliono comunicare in modo sicuro, devono concordare una chiave segreta che verrà utilizzata per cifrare e decifrare i messaggi. Il problema è che se le parti comunicanti condividono la chiave segreta su un canale pubblico, un attaccante potrebbe intercettare la chiave e decifrare i messaggi. L'algoritmo di scambio di chiavi più noto è Diffie-Hellman.
Per capire il funzionamento di Diffie-Hellman occorre introdurre alcuni concetti della matematica modulare. Si intende con \(a \mod n\) il resto della divisione intera di \(a\) per \(n\), ad esempio \(7 \mod 3 = 1\) in quanto il resto della divisione di 7 per 3 è 1. La matematica modulare ci è utile perché alcune operazioni che sono semplici sui numeri reali risultano complesse sui numeri in modulo. Ad esempio, il problema di trovare \(x\) tale che \(a^x = b\) è semplice sui numeri reali, è l'operazione del logaritmo; l'equivalente in matematica modulare invece è estremamente difficile e non si conoscono modi per risolverlo in modo efficiente. Ossia non c'è un algoritmo veloce (il termine corretto è polinomiale) per trovare \(x\) tale che \(a^x \mod n = b\), tale problema è detto problema del logaritmo discreto ed è alla base del funzionamento e della sicurezza di Diffie-Hellman.
Diffie-Hellman
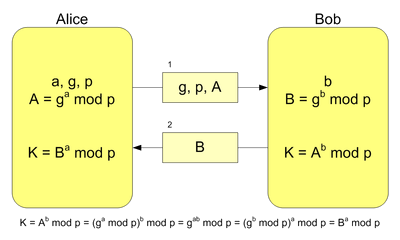
Diamo una rapida panoramica di come funziona Diffie-Hellman, alcuni dettagli tecnici saranno omessi a favore di una spiegazione intuitiva. I passaggi dell'algoritmo sono i seguenti:
- Alice e Bob concordano due parametri: un numero primo \(p\) e un numero \(g\) detto generatore.
- Alice sceglie un numero segreto \(a\) detto chiave privata e calcola \(A = g^a \mod p\), detto chiave pubblica.
- Bob sceglie un numero segreto \(b\) detto chiave privata e calcola \(B = g^b \mod p\), detto chiave pubblica.
- Alice e Bob scambiano i valori \(A\) e \(B\).
- Alice calcola \(s = B^a \mod p\).
- Bob calcola \(s = A^b \mod p\).
- Alice e Bob hanno concordato una chiave segreta \(s\) che possono utilizzare per cifrare e decifrare i messaggi.
L'algoritmo è corretto perché Alice calcola (è sottointesa l'applicazione del modulo) \(s = B^a = (g^b)^a = g^{ab}\) e Bob calcola \(s = A^b = (g^a)^b = g^{ab}\), dunque Alice e Bob concordano la stessa chiave segreta \(g^{ab}\). L'algoritmo è sicuro perché un attaccante che intercetta i valori \(A\) e \(B\) non può calcolare la chiave segreta \(s\) senza conoscere \(a\) o \(b\), e come detto precedentemente non esiste un algoritmo efficiente per risolvere il problema del logaritmo discreto.
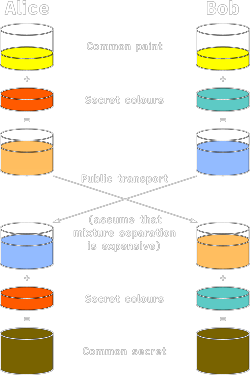
Il paragone che viene fatto spesso per capire il funzionamento di Diffie-Hellman è di immagine i numeri dell'algoritmo come colori e l'operazione di esponenziazione come mescolare i colori. Alice e Bob concordano un colore (il generatore) e un colore di partenza (la chiave privata), e scambiano i colori mescolati (la chiave pubblica). Una volta ricevuto il colore mescolato, Alice e Bob mescolano il colore ricevuto con il proprio colore di partenza e ottengono lo stesso colore, che è la chiave segreta. Ma in tutto questo scambio di colori, un attaccante che intercetta i colori mescolati non può ottenere il colore segreto senza conoscere i colori di partenza.